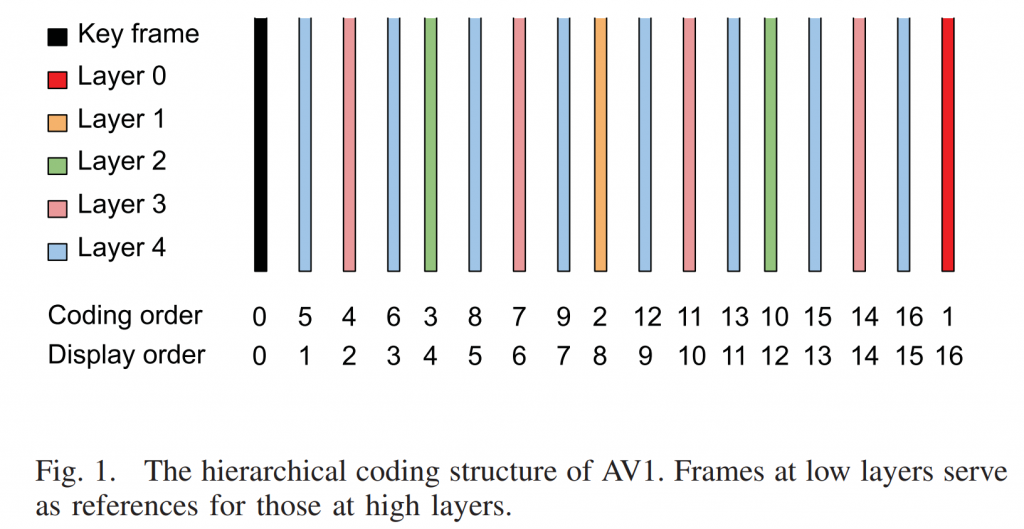
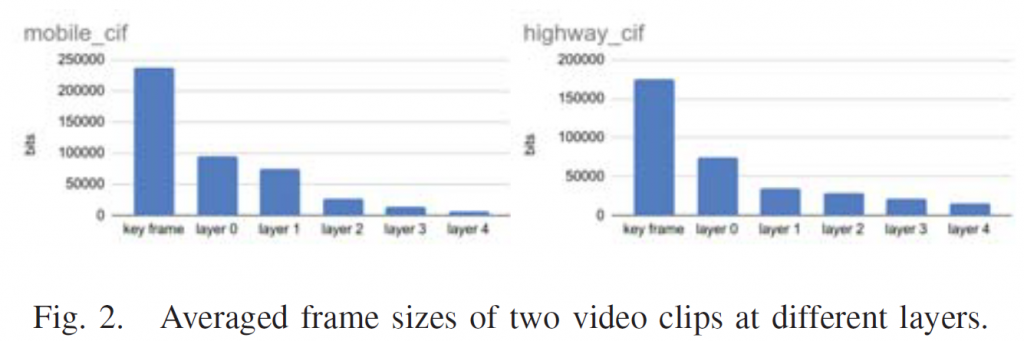
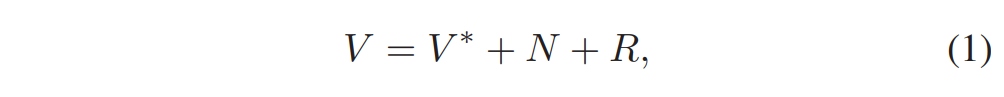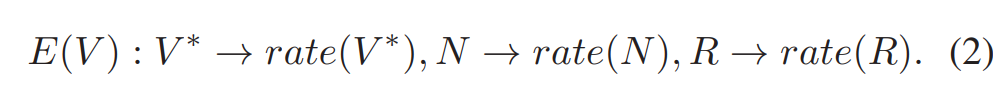1 The six-parameter affine motion model
H. Huang, J. Woods, Y. Zhao, and H. Bai, “Control-point representation and differential coding affine-motion compensation,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 23, no.10, pp.1651–1660, Oct. 2013.
2D 仿射变换被描述为(1-1):
\(\left\{\begin{array}{l}x^{\prime}=a x+b y+e \\ y^{\prime}=c x+d y+f\end{array}\right.\)
其中\((x, y)\)和\(\left(x^{\prime}, y^{\prime}\right)\)分别是当前帧和参考帧中的一对对应位置,\(a 、b、c、d、e\) 和 \(f\) 是仿射参数。 令 \((v_{x}, v_{y})=\) \((x-x^{\prime}, y-y^{\prime})\)为当前帧中位置 \((x, y)\) 的运动,则可以得出(1-2)
\(\left\{\begin{array}{l}
v_{x}=(1-a) x-b y-e \\
v_{y}=(1-c) x-d y-f
\end{array}\right.\)
这称为仿射运动模型(affine motion model)。 与传统的块匹配算法相比,允许参考帧中的匹配块扭曲或变形(warped or deformed),以获得更好的运动补偿预测。 代价是传输更多的运动参数,每块 6 个而不是 2 个。 在视频编码中,运动参数作为辅助信息传输,在较低的总比特率下可能很重要。 因此已经发现,该运动信息的压缩对于提高整体编码性能是至关重要的。 由此产生的运动参数数量的增加可能会抵消仿射运动补偿的优点。因此,运动参数的有效编码对于仿射运动模型变得更加关键。
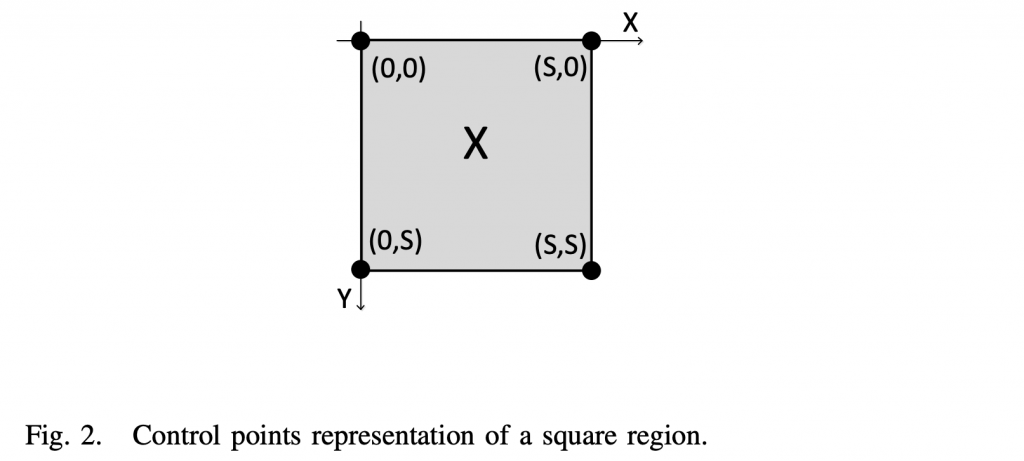
给定一个大小为S × S的正方形区域\(\chi\),设置坐标系如图2所示。顶部和左侧3个角,即\((0,0),(S,0)\)和\( (0,S)\)可以作为控制点,记为\((x_i,y_i),i=0,1,2\)。设它们的平移运动向量为\(\vec{v_i}=(v_{x_i}, v_{y_i}),i=0,1,2\)。矩阵\(\mathbf{V} =(\vec{v}_0,\vec{v}_1,\vec{v}_2)\)称为 affne运动矩阵。 使 \(\chi\) 变形的位移控制点为 \((x_i^{\prime},y_i^{\prime})=(x_i-v_{x_i},y_i-v_{y_i})\)。用\((v_{x_i},v_{y_i})\) 和 \( (x_i,y_i)\)代入(1-2)中的 \((v_x,v_y)\)和\((x,y)\),我们将有六个方程,其中有六个未知数 \(a,b,c,d,e\) 和 \(f\)。 求解这些方程,我们有(1-3):
\(\left\{\begin{array}{l}a=1-\frac{v_{x_1}-v_{x_0}}S,b=\frac{v_{x_0}-v_{x_2}}S,e=-v_{x_0}\\c=1-\frac{v_{y_1}-v_{y_0}}S,d=\frac{v_{y_0}-v_{y_2}}S,f=-v_{y_0}\end{array}\right.\)
通过 (1-2) 和 (1-3),我们得到(1-4):
\(\left\{\begin{array}{l}v_x=\frac{v_{x_1}-v_{x_0}}Sx+\frac{v_{x_2}-v_{x_0}}Sy+v_{x_0}\\v_y=\frac{v_{y_1}-v_{y_0}}Sx+\frac{v_{y_2}-v_{y_0}}Sy+v_{y_0}\end{array}\right.\)
在解码器端接收仿射运动矩阵V,\(\chi\)上的运动场可由(1-4) 导出。
2 The four-parameter affine motion model
L. Li, H. Li, D. Liu, Z. Li, H. Yang, S. Lin, H. Chen, and F. Wu, “An Efficient Four-Parameter Affine Motion Model for Video Coding,” IEEE Transactions on Circuits and Systems for Video Technology, Apr. 2017.
仿射运动模型可以表征平移、旋转、缩放、错切(translation, rotation, zooming, shear mapping)等。 然而,日常视频中最常见的运动仅包括六种典型摄像机运动(camera track, boom, pan, tilt, zoom, and roll)和典型物体运动(平移、旋转和缩放),其中六模型参数超出必要。 需要说明的是,这里的旋转是指物体在与相机平行的二维平面内旋转。 此外,只有当物体与相机之间的相对距离保持不变或者物体具有平坦表面时,才可以使用仿射运动模型来表征物体缩放。 由于本文关注的是局部仿射模型,因此只要局部块足够小,我们就可以假设局部块具有平坦的表面。 下面,将以典型的物体运动为例来解释所提出的四参数仿射运动模型的物理解释。
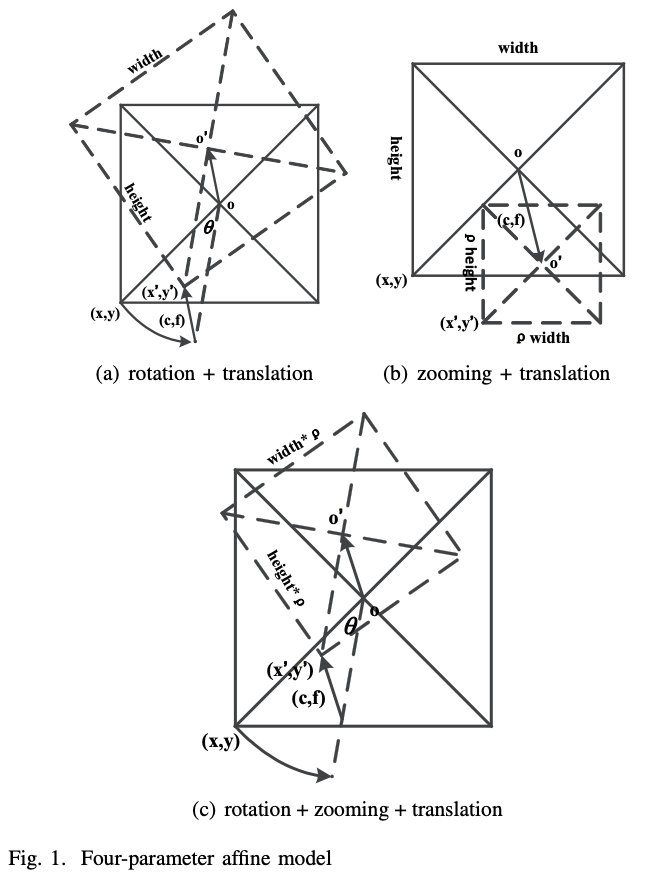
事实上,如图1(a)所示,如果只需要对旋转和平移的组合进行表征,则同一像素变换前后的坐标关系可以描述为(2-2):
\(\left\{\begin{array}{l}x’=\cos\theta\cdot x+\sin\theta\cdot y+c\\y’=-\sin\theta\cdot x+\cos\theta\cdot y+f\end{array}\right.\)
其中 θ 是旋转角度。 此外,如图1(b)所示,如果仅表征缩放和平移的组合,则其关系可以描述为(2-3):
\(\left\{\begin{array}{c}x’=\rho\cdot x+c\\y’=\rho\cdot y+f\end{array}\right.\)
其中 ρ 分别是 x 和 y 方向上的缩放因子。
旋转/缩放和平移的组合都需要三个参数来表征。 如果我们将旋转、缩放和平移结合在一起,则需要四个参数,其关系可以描述为(2-4):
\(\left\{\begin{array}{l}x^{\prime}=\rho\cos\theta\cdot x+\rho\sin\theta\cdot y+c\\y^{\prime}=-\rho\sin\theta\cdot x+\rho\cos\theta\cdot y+f\end{array}\right.\)
如果我们将 ρcos θ 和 ρsin θ 替换为 (1 + a) 和 b,则 (2-4) 可以重写为(2-5):
\(\left\{\begin{array}{l}MV_{(x,y)}^h=x^{\prime}-x=ax+by+c\\MV_{(x,y)}^v=y^{\prime}-y=-bx+ay+f\end{array}\right.\)
其中\(MV_{(x,y)}^h\)和\(MV_{(x,y)}^v\) 是位置 (x, y) 的 MV 的水平和垂直分量。 等式(2-5)是采用的四参数仿射运动模型,能够精确表征旋转、缩放和平移的组合。
六参数仿射运动模型与四参数仿射运动模型进行比较,可以明显看出,在四参数仿射运动模型下,每个块计算的参数较少,因此解码复杂度可以稍微降低。 此外,由于稍后将介绍的快速仿射ME算法可以在四参数仿射运动模型下更快地收敛,因此编码复杂度也将降低。 由于标头信息的比特节省,四参数仿射运动模型可以为大多数自然序列带来更好的 R-D 性能。
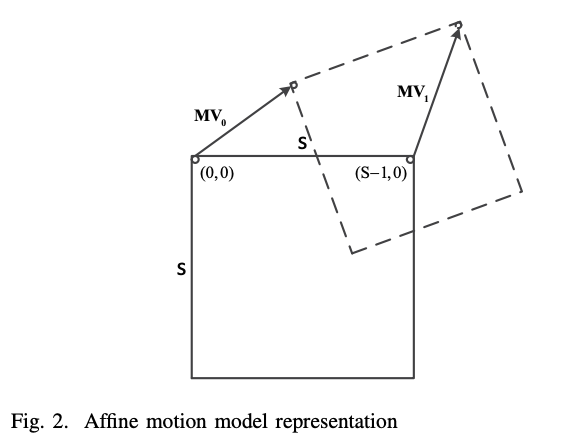
根据式(2-5),有四个未知模型参数。 除了这四个参数,我们还可以使用两个MV来等效地表示模型,因为使用MV更符合现有的视频编码框架。 可以在当前块的任何位置选择这两个 MV 来表示运动模型。 我们选择当前块的左上和右上位置的MV,因为这两个位置与先前重建的块相邻,并且可以更准确地预测对应的MV。 在如图 2 所示的典型 S × S 块中,如果我们将左上角像素 (0, 0) 的 MV 表示为 MV0,将右上像素 (S − 1, 0) 的 MV 表示为 MV1,则模型参数a、b、c、f可根据式(5)求解如下(2-6):
\(\left\{\begin{array}{ll}a=\frac{MV_1^h-MV_0^h}{S-1}&c=MV_0^h\\b=-\frac{MV_1^v-MV_0^v}{S-1}&f=MV_0^v\end{array}\right.\)
3 Affine Motion Eestimate
下面给出VTM中4参数和6参数Affine ME的迭代步骤:
步骤1:寻找ME过程的初始CPMV。 测试若干个候选的CPMV组合,对于每个候选,通过将CPMV设置为候选MV来执行当前块的AMC,然后计算AMC预测块的SATD成本。 初始CPMV候选设置为等于提供最小 SATD 成本的候选者。
步骤2:从仿射参数Pi推导Pi+1。那么当使用Pi+1进行AMC时当前块的总误差可以计算为(3-3)
\(D=\sum_{(x,y)\in B}\lVert org(x,y)-ref(W(x,y,P_{i+1}))\rVert^2\)
其中对于6参数模型(3-4):
\(\left.W=\left[\begin{array}{c}ax+by+e\\cx+dy+f\end{array}\right.\right]=\left[\begin{array}{cccccc}x&0&y&0&1&0\\0&x&0&y&0&1\end{array}\right]\left[\begin{array}{ccccc}a&c&b&d&e&f\end{array}\right]^T\)
对于6参数模型(3-5):
\(\left.W=\left[\begin{matrix}ax+by+e\\-bx+ay+f\end{matrix}\right.\right]=\left[\begin{matrix}x&y&1&0\\-y&x&0&1\end{matrix}\right]\left[\begin{array}{cccc}a&b&e&f\end{array}\right]^T\)
将(3-3)改写为(3-6):
\(D=\sum_{(x,y)\in B}\lVert org(x,y)-ref(W(x,y,P_i+\Delta P))\rVert^2\)
将\(ref(W(x,y,P_i+\Delta P))\)泰勒展开得(3-7):
\(ref(W(x,y,P_i+\Delta P))\approx ref(W(x,y,P_i))+\frac{\partial ref}{\partial W}\frac{\partial W}{\partial P}\Delta P\)
其中\(\frac{\partial ref}{\partial W}\)为参考图像对位置的导数,即梯度\(\begin{matrix}G=[G_x&G_y]\end{matrix}\); \(\frac{\partial W}{\partial P}\)可以由(3-4)(3-5)推导,因此对于6参数模型(3-8):
\(Q(x,y)=\frac{\partial ref}{\partial W}\frac{\partial W}{\partial P}=\begin{matrix}[xG_x&xG_y&yG_x&yG_y&G_x&G_y]\end{matrix}\)
对于4参数模型(3-9):
\(Q(x,y)=\frac{\partial ref}{\partial W}\frac{\partial W}{\partial P}=\begin{matrix}[xG_x-yG_y&yG_x+xG_y&G_x&G_y]\end{matrix}\)
带入(3-8)或(3-9)到(3-6)中得(3-9):
\(D=\sum_{(x,y)\in B}\lVert E(x,y)-Q(x,y)\Delta P\rVert^2\)
其中\(E(x,y)=org(x,y)-ref(W(x,y,P_i)\)。
求D的最小值即可得到\(\Delta P\),我们对D求导并令导数为0得(3-10):
\(Q^TQ\Delta P=Q^TE\)
其中Q是尺寸为m×6或者m×4的矩阵,E是长度m×1的向量,m是CU内的像素总数。使用高斯消元法可得到\(\Delta P\),则可推导出\(P_{i+1}=P_i+\Delta P\)。
步骤3:使用\(P_{i+1}\)执行当前块的AMC,然后计算AMC预测块的SATD成本C(i+1)。 如果 C(i+1) < C*,则 C*设置为等于 C(i+1)。
步骤4:若\(P_{i+1}\)与\(P_i\)不相同且i小于最大迭代次数,则设i=i+1,转步骤2; 否则,终止ME过程。